Innowacyjny monitoring betonu na przykładzie budowy mostu nad Odrą w Raciborzu

Uzyskanie skutecznego odwodnienia oraz prawidłowej zabudowy elementów wyposażenia wymaga zwiększenia grubości warstwy wiążącej i jej różnicowania na długości. Prawidłowa niweleta na obiekcie wpływa na bezpieczeństwo i komfort użytkowników (ryc. 1).

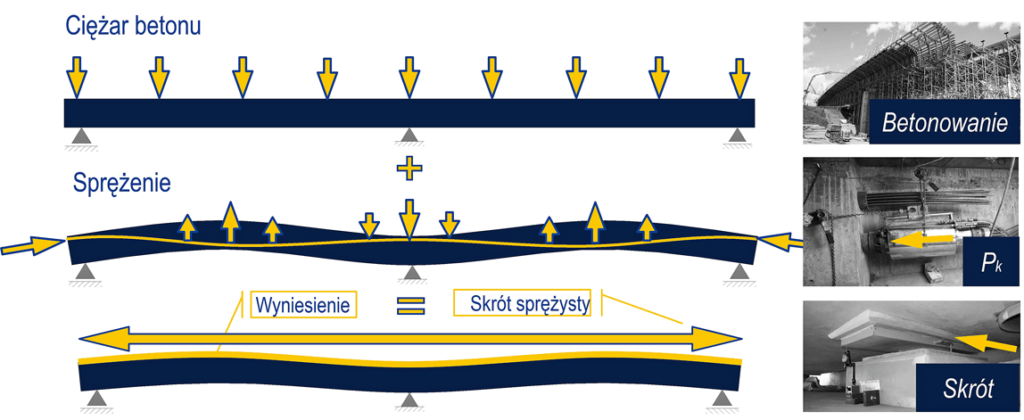
Spełnienie projektowanych parametrów geometrycznych ustroju nośnego wymaga weryfikacji założeń normowych z uwzględnieniem receptury betonu. Wpływ kruszyw stosowanych powszechnie w mostownictwie może zmieniać odkształcalność betonu nawet o 100% przy spełnieniu pozostałych parametrów [1, 2]. Beton z kruszywem granitowym charakteryzuje się dużą odkształcalnością z modułami poniżej 30 GPa. Do grupy kruszyw o niskiej odkształcalności betonu zaliczamy bazalt, amfibolit, dolomit i wapień z modułami sprężystości dochodzącymi do 50 GPa. Podczas budowy mostów z betonu sprężonego powinny być stosowane metody identyfikacji odkształcalności betonu podczas ich wznoszenia.

Badania laboratoryjne odkształcalności betonu powinny być wykonywane z uwzględnieniem warunków panujących podczas betonowania i okresu dojrzewania betonu. W przypadku dźwigarów mostowych z betonu sprężonego mamy do czynienia z masywnymi elementami, w których uzyskujemy wysokie temperatury podczas wiązania betonu. Ciepło wiązania po ok. 30 h powoduje wzrost temperatury nawet do ponad 70 °C [3–5] w zależności od okresu betonowania. Korzystny wpływ ciepła wiązania na wczesną wytrzymałość betonu [2, 6–8] powinien być również uwzględniany w badaniach laboratoryjnych przez odpowiedni sposób pielęgnowania próbek do badań. Wymaga to jednak zastosowania systemu monitorowania cech betonu, który pozwala odwzorować warunki panujące na budowie. W ten sposób uzyskujemy miarodajne parametry wytrzymałości betonu we wczesnym wieku, do 7 dni. Dzięki temu można minimalizować ryzyka związane z podejmowaniem decyzji na budowie. Skracanie czasu na realizację kolejnych etapów dodatkowo zmniejsza koszty budowy.

Próbne obciążenia mostów prowadzone przez akredytowane laboratorium Politechniki Śląskiej potwierdzają uzyskiwanie zmiennych odkształcalności przęseł podczas kontrolowanych wymuszeń statycznych. W zależności od zastosowanej receptury betonu relacja ugięć sprężystych w stosunku do ugięć teoretycznych w skrajnych przypadkach wynosi od 50% do nawet 120%. Przykładem jest most drogowy MS-6B w ciągu S7 na obwodnicy Ostródy (ryc. 2). Dla lewej jezdni zastosowano beton C50/60 na kruszywie granitowym z kopalni Siedlimowice charakteryzujący się dużą odkształcalnością. Uzyskana zgodność ugięć sprężystych do wartości teoretycznych wyniosła do 115%. Podczas budowy jezdni prawej zmieniono w recepturze kruszywo na bazaltowe o niskiej odkształcalności. Badania odbiorcze wykazały zgodność sztywności giętnej do 89% wartości teoretycznej.

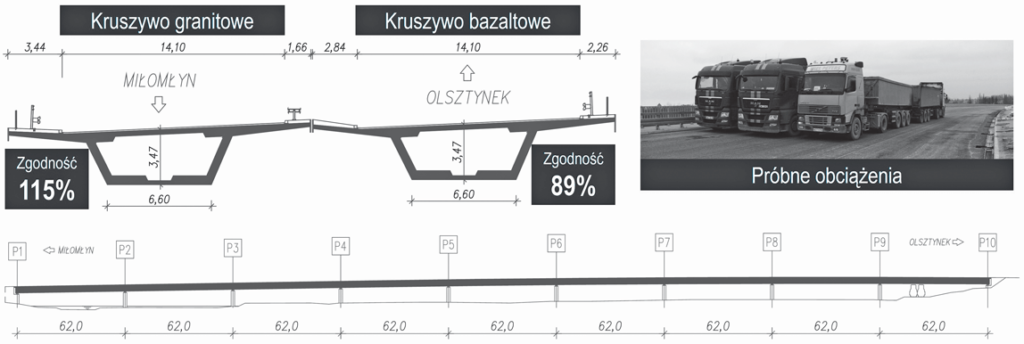
Obserwowane różnice w sztywności giętnej przęseł skłoniły autorów do opracowania własnej metody identyfikacji odkształcalności betonu w badaniach laboratoryjnych z uwzględnieniem sposobu pielęgnacji próbek. Skuteczne wdrożenie procedury zostało zrealizowane podczas budowy obiektów mostowych na obwodnicy Raciborza. W celu uzyskania zbliżonych warunków pielęgnacji próbek w laboratorium zastosowano innowacyjny system monitorowania temperatury dojrzewania betonu połączony automatycznie ze sterowaniem pieca. Uzupełnieniem systemu była procedura postępowania na potrzeby określania cech mechanicznych betonu w warunkach odwzorowanych.

Odkształcalność betonu w normatywach

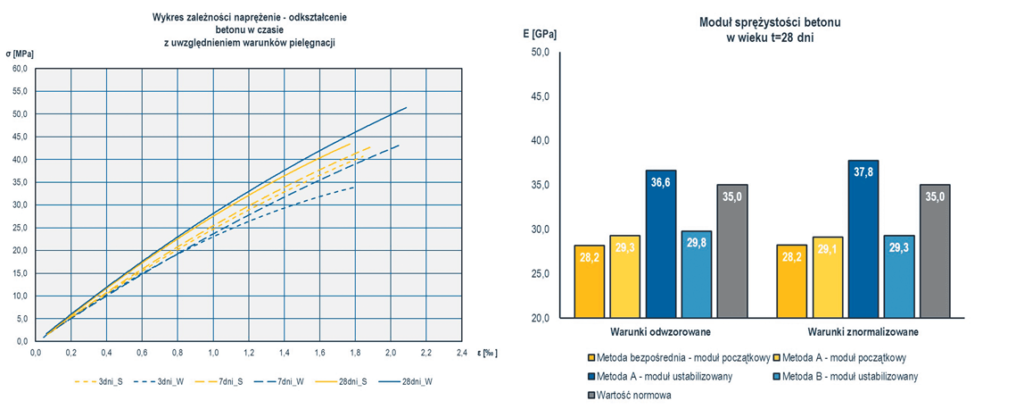
Moduł sprężystości jest zależnością odkształcenia ε w materiale liniowo-sprężystym od naprężenia σ, jakie w nim występuje. Na wykresie moduł sprężystości jest kątem nachylenia prostej σ–ε w stosunku do poziomej osi odkształcenia. W praktyce inżynieryjnej normatywy dopuszczają prawo Hooke’a z liniowym odcinkiem krzywej σ–ε. Moduł sprężystości przyjmuje się jako wartość sieczną pomiędzy początkiem układu współrzędnych a ustalonym poziomem naprężeń (ryc. 3).

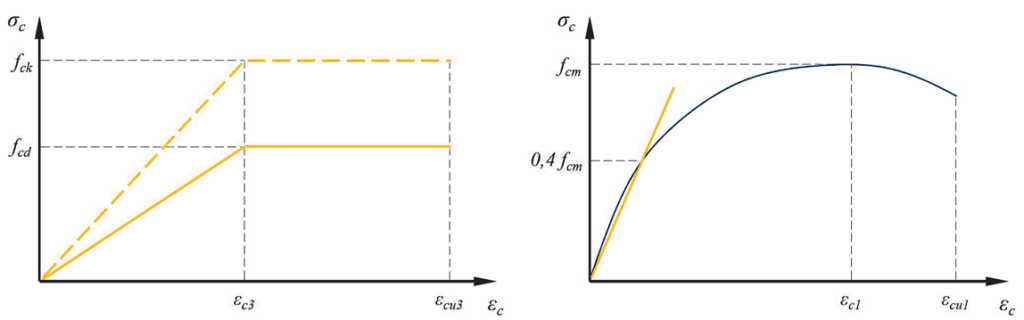
W obowiązującej w Polsce normie PN-EN 1992-1-1 [9] wartość modułu sprężystości betonu E_cm zdefiniowano jako wartość sieczną dla przedziału naprężeń od 0,5 MPa do 0,4 f_cm zgodnie ze wzorem:

E_cm = 22 (0,1 f_cm)^0,3 [GPa]

gdzie:
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych.

Podkreślono zależność wartości modułu od składu mieszanki ze szczególnym uwzględnieniem kruszywa. Wzór określający wartość modułu sprężystości odniesiono do betonu z kruszywem kwarcytowym. Dla betonów z kruszywem wapiennym i piaskowcowym wartości te należy zmniejszyć odpowiednio o 10% i 30%. Dla kruszyw bazaltowych wartość modułu należy zwiększyć o 20%. Brak jest wytycznych modyfikacji wartości modułu sprężystości dla powszechnie stosowanych w Polsce kruszyw: granitowego, granodiorytowego, porfirowego, amfibolitowego czy dolomitowego.

Mosty sprężone w procesie projektowania i budowy można uznać za konstrukcje wrażliwe na odchylenia wartości modułu sprężystości. Norma zaleca oszacować odkształcalność betonu „z uwzględnieniem specyfiki zagadnienia” na podstawie badań laboratoryjnych. W projekcie nowej wersji Eurokodu 2 (prEN 1992-1-1[10]) już doprecyzowano, że w przypadku tego typu konstrukcji wartość modułu sprężystości powinna być zapisana w specyfikacji lub określona na podstawie badań. Wprowadzony został współczynnik k_E. Jego wartość określana jest na podstawie rodzaju kruszywa. Podana została tylko wartość współczynnika k_E dla kruszywa kwarcytowego i wynosi ona 9500. Dla innych kruszyw podano informację, że wartość współczynnika k_E waha się między 5000 a 13 000. Ich określenie w zależności od rodzaju kruszywa może być zapisane w załączniku krajowym. Przeliczając podane wartości na modyfikację bazowej wartości modułu sprężystości, analogicznie jak jest to przedstawione w aktualnej wersji EC2, wartość minimalna to -47%, a wartość maksymalna +37%.

E_cm = k_E f_cm ^1/3 [MPa]

gdzie:
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych,
k_E [ – ] – współczynnik zależny od zastosowanego kruszywa.

Obecnie stosowany Model Code 2010 [11] stworzony przez fib rozróżnia dwie wartości modułu sprężystości. Pierwsza z nich – E_ci – zdefiniowana jest jako wartość styczna w punkcie początkowym wykresu σ–ε. Jest to wartość w przybliżeniu równa nachyleniu krzywej σ–ε przy odciążaniu i nie uwzględnia początkowych odkształceń plastycznych. Jest ona określona wzorem:

E_ci = E_c0 α_E (f_cm / 10) ^1/3 [GPa]

gdzie:
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych,
E_c0 = 21,5 [GPa] – wartość bazowa modułu sprężystości betonu,
α_E [ – ] – współczynnik zależny od zastosowanego kruszywa.

Druga wartość modułu sprężystości E_c zdefiniowana jest jako wartość sieczna dla przedziału naprężeń od 0 MPa do 0,4 f_cm. Określono ją jako zredukowaną wartość E_ci, uwzględniającą początkowe odkształcenie plastyczne w betonie oraz wynikające z niej deformacje nieodwracalne. Wartość ta jest zalecana do wykorzystania w przypadku sprężystej analizy numerycznej według wzoru:

E_c = α_i E_ci [GPa]

gdzie:
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych.

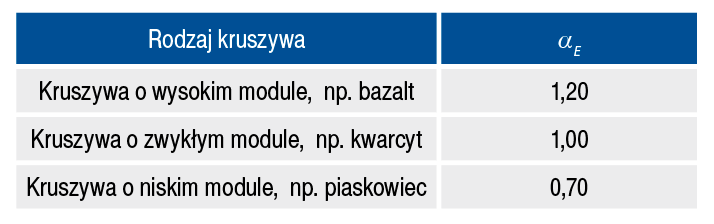
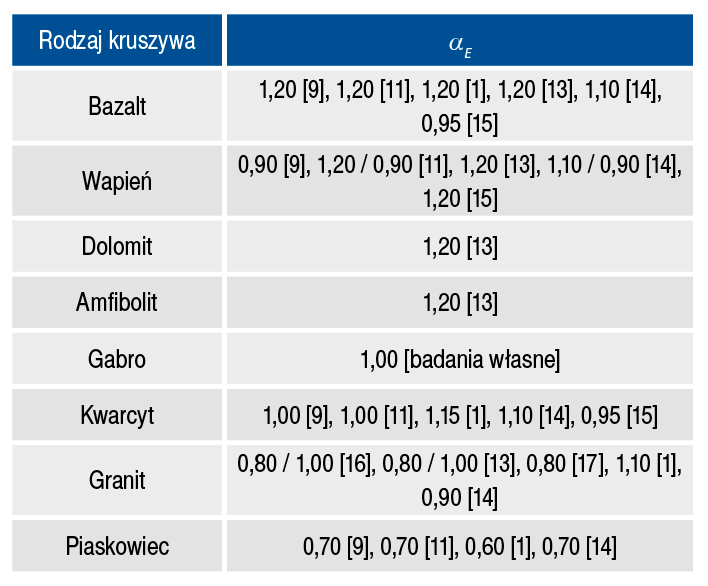
W tabeli 2 przedstawiono wartości współczynnika α_E w zależności od normatywów. Z uwagi na rozbieżności w przypadku konstrukcji wrażliwych na odchylenia od wartości ogólnych zalecone jest, aby moduł sprężystości był szczegółowo określony lub wyznaczony doświadczalnie. Podobnie jak w przypadku Eurokodu 2, brak jest wartości współczynnika α_E dla powszechnie obecnie stosowanych w Polsce kruszyw. Projekt nowej wersji dokumentu fib Model Code 2020 [12] dla modułu sprężystości betonu zmienia jedynie tabelę ze współczynnikami α_E (tab. 1). Wprowadzono trzy grupy kruszyw: kruszywa o wysokim module, kruszywa o zwykłym module oraz kruszywa o niskim module. Nie ma w niej już przypisanych wartości współczynnika do konkretnego rodzaju kruszywa. Jako przykładowe kruszywa dla poszczególnych grup podano odpowiednio bazalt, kwarcyt i piaskowiec. Uzupełnieniem do tabeli jest informacja o właściwościach kruszyw mogących znacząco się różnić w zależności od miejsca wydobycia. Jest to istotna informacja, która sprawia, że nawet wiedza o rodzaju kruszywa nie jest wystarczająca do właściwego oszacowania wartości modułu sprężystości.

Amerykańska norma dotycząca mostów betonowych ACI 343R [18] definiuje moduł sprężystości po przekształceniu do jednostek systemu SI następująco:

E_cm = 𝜌_c^1,5 0,0428 √𝑓_cm [MPa]

gdzie:
𝜌_c [kg/m³] – gęstość objętościowa betonu,
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych.

Amerykańskie wytyczne do projektowania mostów na drogach szybkiego ruchu AASHTO LRFD Bridge Design Specifications [19] po przekształceniu do jednostek systemu SI oraz z zastosowaniem oznaczeń wykorzystywanych w Eurokodzie 2 przyjmują postać:

E_cm = 0,00171 𝐾₁ 𝜌_c² 𝑓_cm ^0,33 [MPa]

gdzie:
𝐾₁ – współczynnik korygujący wartość modułu z uwagi na źródło pochodzenia kruszywa,
𝜌_c [kg/m³] – gęstość objętościowa betonu,
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych.

Norma australijska AS 3600 [20] podaje, że wartość modułu sprężystości powinna być wyznaczona na lub zgodnie z podanymi wzorami albo podstawie badań laboratoryjnych. Jako jedyna rozróżnia wartość modułu sprężystości dla przedziałów wytrzymałości na ściskanie:

E_cm = 𝜌_c^1,5 0,043 √𝑓_cm [MPa] dla 𝑓_cm ≤ 40 MPa
E_cm = 𝜌_c^1,5 (0,024 √𝑓_cm + 0,12) [MPa] dla 𝑓_cm > 40 MPa

gdzie:
𝜌_c [kg/m³] – gęstość objętościowa betonu,
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych.

Kanadyjska norma CSA A23.3 [21] zaleca określanie modułu sprężystości betonu przyjmowany do obliczeń na podstawie badań laboratoryjnych betonu. Dodatkowo jeśli wartość modułu sprężystości jest kluczowa, to powinna ona być zapisana w specyfikacji oraz umieszczona na rysunkach. Jeśli nie wykonuje się badań laboratoryjnych, można wykorzystać jeden ze wzorów:

E_cm = (3300 √𝑓_cm + 6900) (𝜌_c/2300 )^1,5 [MPa]
E_cm = 4500 √𝑓_cm [MPa] dla 𝑓_cm ≤ [MPa]

gdzie:
𝜌_c [kg/m³] – gęstość objętościowa betonu,
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych.

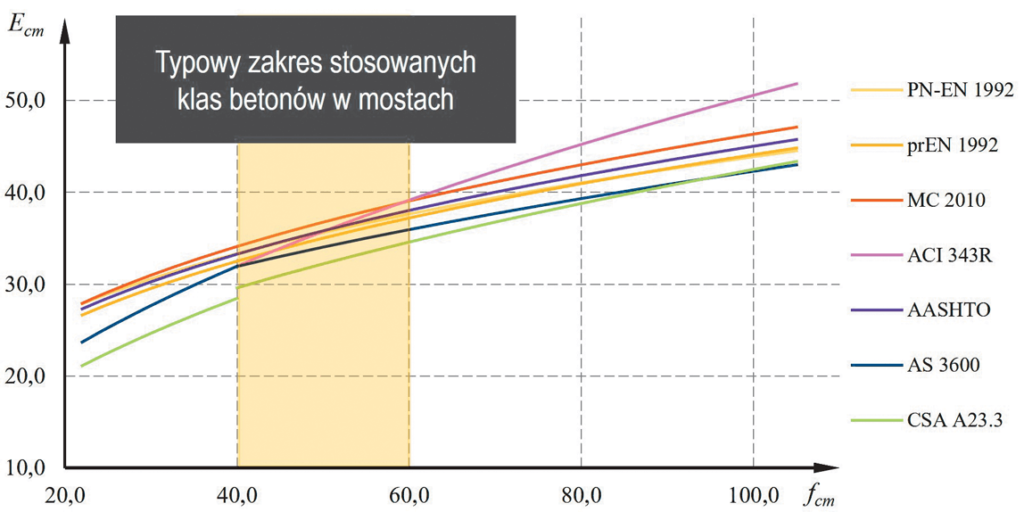
Reasumując, stosowane normatywy zwracają uwagę na zasadność określania odkształcalności betonu laboratoryjnie (ryc. 4). Dostrzeżony jest fakt istotnych różnic modułu w zależności od stosowanych kruszyw. Jednak nie ma informacji o konieczności uwzględniania wpływu ciepła wiązania betonu na jego cechy mechaniczne oraz sposobu pielęgnacji próbek. Uwzględniając powyższe, autorzy wraz z firmami STRABAG i TPA przeprowadzili szereg badań podczas budowy obiektów mostowych w celu identyfikacji odkształcalności betonu. Opis procedury wraz z wynikami badań przedstawiono w dalszej części artykułu.

Własna metoda badań

Identyfikacja odkształcalności betonu w procesie budowy mostów betonowych wymaga stosowania metody uwzględniającej czynniki wpływające na końcową wartość. Zatwierdzenie receptury betonu powinno uwzględniać dobór składników wpływających na cechy mechaniczne związane z wczesnym (3–7 dni) przyrostem wytrzymałości na ściskanie i odpowiadającym modułem sprężystości oraz uzyskiwanym ciepłem wiązania w konstrukcji. Podejmowanie decyzji o sprężeniu lub zwolnieniu rusztowań odbywa się minimum po 3 dniach w zależności od stosowanej technologii. Uwzględniając spostrzeżenia wykonawców i projektantów w procesie budowy mostów betonowych, zaproponowano metodę identyfikacji odkształcalności betonu na potrzeby podejmowania decyzji. Poniżej przedstawiono diagram ilustrujący proces podejmowania decyzji (ryc. 5).

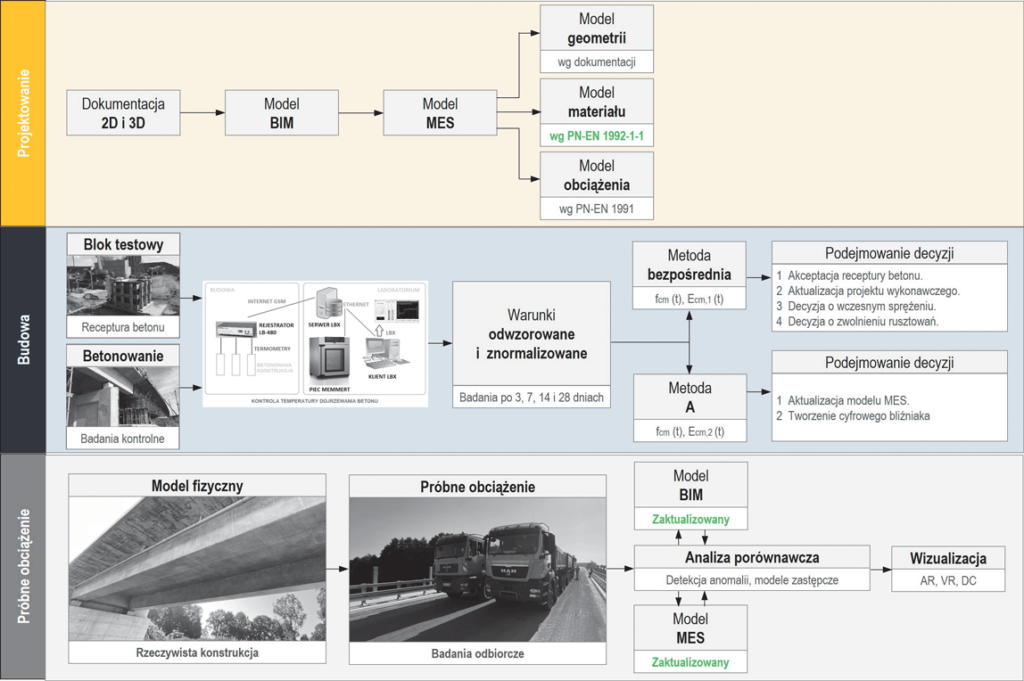
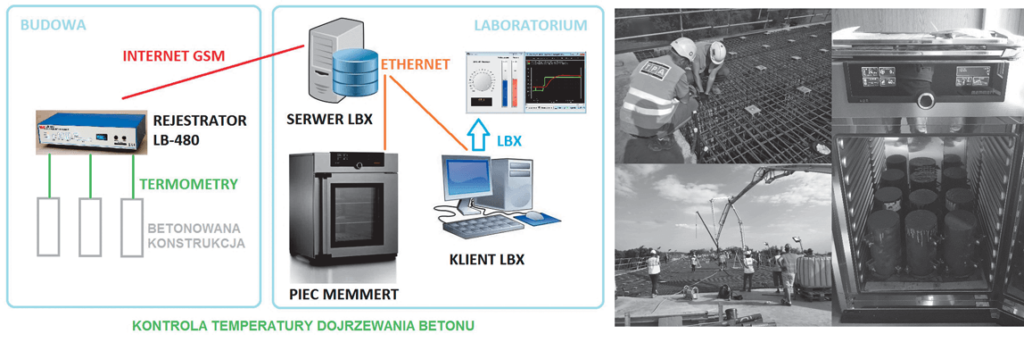
Badania składają się z dwóch etapów. Etap 1 należy przeprowadzać na bloku testowym w celu podjęcia decyzji o zatwierdzeniu receptury, uwzględniając technologię budowy i związane z tym oczekiwania projektanta i wykonawcy. Wymiar bloku powinien być ustalany indywidualnie na podstawie geometrii dźwigara. Autorzy proponują blok o wymiarach 1,2 m x 1,2 m x 1,2 m. Etap 2 dotyczy kontroli podczas betonowania ustroju nośnego. Uzyskanie warunków odwzorowujących dojrzewanie betonu realizowane jest z wykorzystaniem innowacyjnego systemu monitoringu. System składa się z czujników temperatury umieszczonych w bloku testowym i konstrukcji, rejestratora LB-480, serwera LBX oraz pieca Memmerta. Dzięki rejestracji temperatury w elemencie system steruje piecem, uzyskując zbliżone warunki pielęgnacji próbek w laboratorium (ryc. 6).

Przygotowanie próbek oraz badania niszczące należy wykonywać z obowiązującymi normami PN-EN. Do badań w jednym cyklu betonowania należy przyjąć min. 24 sztuki próbek walcowych o średnicy d = 150 mm i wysokości h = 300 mm. W warunkach znormalizowanych pielęgnujemy 12 próbek przechowywanych w wodzie. Warunki odwzorowane dotyczą próbek przechowywanych w suszarce sterowanej temperaturą wiązania do 7 dni. W pozostałym okresie próbki zabezpieczone przed utratą wilgotności mogą być przechowywane w temperaturze pokojowej ok. 20 °C. 

Badania niszczące na bloku testowym określające zależność naprężenie – odkształcenie należy wykonać po 3, 7, 14 i 28 dniach dojrzewania. Podczas betonowania przęseł badania kontrolne należy wykonywać po 3, 7 i 28 dniach lub ustalając na podstawie przyjętych etapów robót. Pomiar odkształceń powinien być realizowany wzdłuż trzech linii rozmieszczonych na pobocznicy co 120°.

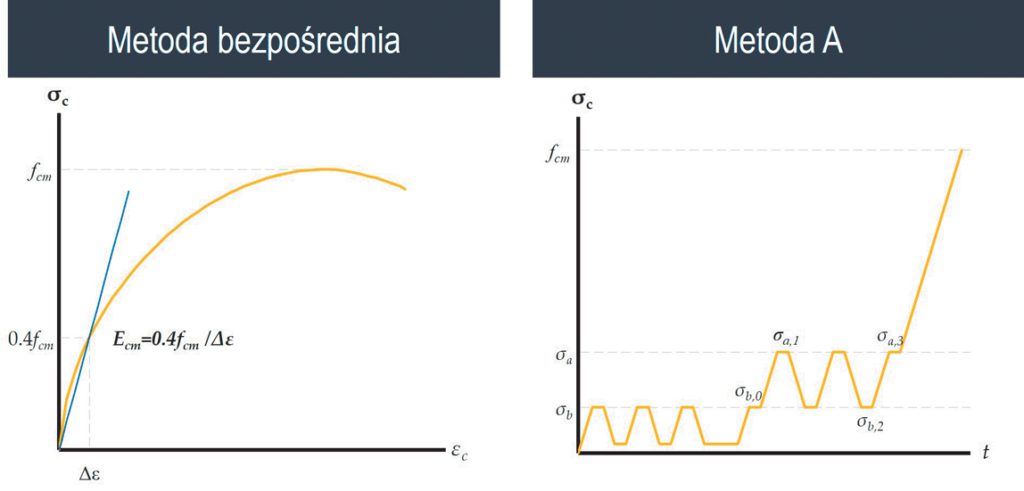
Analizę cech mechanicznych betonu należy przeprowadzać z wykorzystaniem metody bezpośredniej z uwzględnieniem normy PN-EN 1992-1-1 [9] oraz metody A zgodnie z normą PN-EN 12390-13 [22]. Metoda bezpośrednia związana jest z jednym cyklem przyrostu naprężenia do zniszczenia. Określenie siecznego modułu sprężystości betonu odbywa się bez eliminacji odkształceń trwałych (plastycznych), co odpowiada pierwszemu obciążeniu stwardniałego betonu podczas procesu sprężania lub zwolnienia rusztowań. Poniżej przedstawiono stosowane wzory:

E_cm = 0,4𝑓_cm/𝛥𝜀 [GPa]
𝛥𝜀 = 𝛥𝑙/𝑙_o [GPa]

gdzie:
f_cm [MPa] – średnia wytrzymałość betonu na ściskanie określona na próbkach walcowych,
𝛥𝜀 – przyrost odkształcenia próbki betonowej wywołany osiągnięciem 0,4f_cm,
𝛥𝑙 – zmiana długości próbki wywołana osiągnięciem 0,4f_cm,
 𝑙_o – długość próbki walcowej.

Do wyznaczenia siecznego modułu sprężystości betonu z eliminacją odkształceń trwałych przyjęto znormalizowaną metodę A. Odpowiada sytuacji użytkowej, w której przęsła mostów poddawane są cyklicznym oddziaływaniom użytkowym. Konstrukcje sprężone mają już wyeliminowane odkształcenia trwałe, gdzie przekrój poddawany jest zmianom naprężeń ściskających w zakresie liniowym. Określenie modułu początkowego E_c,o i ustabilizowanego E_c,s zrealizowano zgodnie z procesem obciążania przedstawionym na rycinie 7. Przy obliczaniu modułu skorzystano ze wzorów:

E_c,s = 𝜎^m_a,3 – 𝜎^m_b,2/𝜀^m_a,3 – 𝜀^m_b,2 [GPa]

gdzie:
𝜎^m_a,3 – 𝜎^m_b,2 – zarejestrowane naprężenia z przedziału 1/3·f_cm i (0,10÷0,15) f_cm,
𝜀^m_a,3 – 𝜀^m_b,2 – zarejestrowane odkształcenia z przedziału 1/3·f_cm i (0,10÷0,15)·f_cm.

Na potrzeby podejmowania decyzji o sprężeniu lub zwolnieniu rusztowań podczas budowy przyjęto wyniki badań wytrzymałości na ściskanie betonu dla próbek pielęgnowanych w warunkach odwzorowanych. W celu aktualizacji określenia podniesienia wykonawczego oraz programu sprężania zaleca się przyjęcie wartości modułu sprężystości betonu E_cm,1 określonego metodą bezpośrednią (bez eliminacji odkształceń trwałych) dla próbek pielęgnowanych w warunkach odwzorowanych. Na potrzeby aktualizacji analiz konstrukcji w fazie użytkowej (po eliminacji odkształceń trwałych) zaleca się przyjęcie wartości modułu sprężystości betonu E_cm,2 określonego metodą A na próbkach po 28 dniach pielęgnowania w warunkach odwzorowanych. W przypadku wykonywania próbnych obciążeń ostateczna weryfikacja odbywa się z uwzględnieniem wyników badań in situ po uwzględnieniu wpływu wyposażenia oraz stopnia zbrojenia.

Wyniki badań

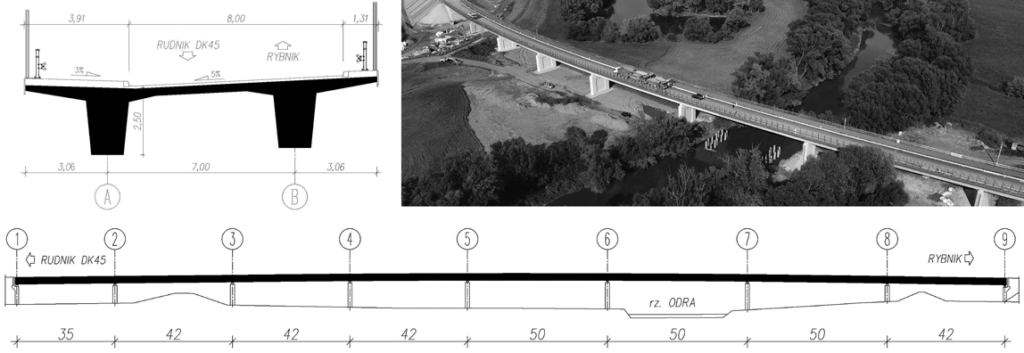
Wdrożenie procedury zostało zrealizowane podczas budowy obiektów mostowych na obwodnicy Raciborza. Jednym z obiektów była konstrukcja nośna mostu MG-1 tworząca ośmioprzęsłowy, ciągły ustrój nośny z betonu sprężonego klasy C40/50. Rozpiętość teoretyczna przęseł wynosi 35,00 + 3 x 42,00 + 3 x 50,00 + 42,00 m. Całkowita szerokość obiektu jest równa 13,22 m. Przez obiekt prowadzona jest dwukierunkowa jezdnia o szerokości 8,00 m, każda z obustronną zabudową chodnikową, barierami energochłonnymi i balustradami. Ustrój nośny stanowią dwie belki o przekroju trapezowym w rozstawie osiowym 7,0 m, połączone żelbetową płytą pomostową o grubości 0,30 m. Belki mają szerokości 1,20 m u dołu oraz wysokość 2,50 m. Płyta pomostowa między dźwigarami ma przy belkach skosy zwiększające jej grubość do 0,50 m. Obustronne wsporniki mają wysięg 2,26 m. W osiach podpór zaprojektowano poprzecznice o szerokości 0,80 m i wysokości 2,20 m. Przęsła podparte są na podporach za pomocą dwóch łożysk garnkowych na każdej podporze (ryc. 8).

Do obliczeń przyjęto model MES prętowo-powłokowy klasy (e¹ + e²p³; ryc. 9). Dźwigary główne oraz poprzecznice odwzorowano elementami prętowymi z parametrami geometrycznymi uwzględniającymi współpracę płyty pomostowej. Płytę pomostową odwzorowano elementami powłokowymi z wyłączeniem sztywności na kierunku podłużnym i pozostawieniem pełnej sztywności na kierunku poprzecznym. W modelu materiału jako odniesienie normowe przyjęto moduł sprężystości betonu równy 39,0 GPa.

Blok testowy został zabetonowany 27 kwietnia 2020 r. Wbudowano mieszankę o konsystencji S3 (opad stożka 110 mm), zawartości powietrza 5,0% i temperaturze 19,0 °C. Maksymalna temperatura o wartości 62,0 °C została osiągnięta po 32 h od zabetonowania bloku. Badania te zostały wykonane na potrzeby określenia podniesienia wykonawczego, aktualizacji programu sprężania oraz decyzji o wczesnym sprężeniu po 3 lub 7 dniach. Wytrzymałość betonu oraz moduł sprężystości z wykorzystaniem metody bezpośredniej przeprowadzono w wieku 3, 7, 14, 28 i 90 dni. 

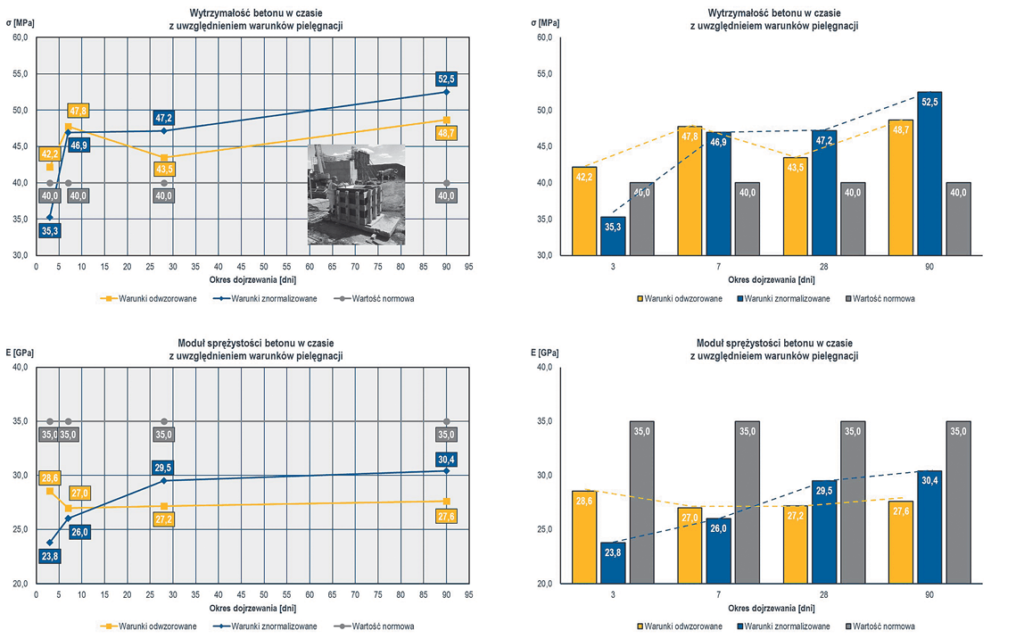
Zestawione wyniki badań z bloku testowego (ryc. 10) potwierdziły wpływ temperatury wiązania na początkowy przyrost wytrzymałości betonu na ściskanie f_cm(t). Dla próbek pielęgnowanych w warunkach odwzorowanych już po trzech dniach uzyskano 42,02 MPa (wymagane 40 MPa). Po 7 dniach nastąpił przyrost do 47,8 MPa, a w kolejnych dniach nie zaobserwowano istotnego wpływu wieku na dalszy wzrost wytrzymałości. Nieco inne wynik uzyskano dla próbek pielęgnowanych w wodzie. Po 3 dniach uzyskano jedynie 35,3 MPa, nie spełniając wymaganych 40 MPa. Dopiero po 7 dniach uzyskana wartość wynosiła 46,9 MPa. W funkcji wieku uzyskano dalszy wzrost wytrzymałości do 52,5 MPa po 90 dniach dojrzewania. W przypadku modułu sprężystości betonu E_cm,1 określonego metodą bezpośrednią dla próbek pielęgnowanych w warunkach odwzorowanych po 3 dniach uzyskano wartość 28,6 GPa, a po 28 dniach wartość modułu wyniosła 27,2 GPa. Dla próbek pielęgnowanych w warunkach znormalizowanych dostrzec można wpływ wieku na wzrost wartości modułu. Po 3 dniach uzyskano wartość 23,8 GPa, a po 7, 28 i 90 dniach odpowiednio 26,0 GPa, 29,5 GPa i 30,40 GPa. Na potrzeby podejmowania decyzji na budowie o terminie sprężania za miarodajne uznano wyniki badań dla próbek pielęgnowanych w warunkach odwzorowanych. Określony moduł sprężystości betonu posłużył do aktualizacji programu sprężania oraz podniesienia wykonawczego.

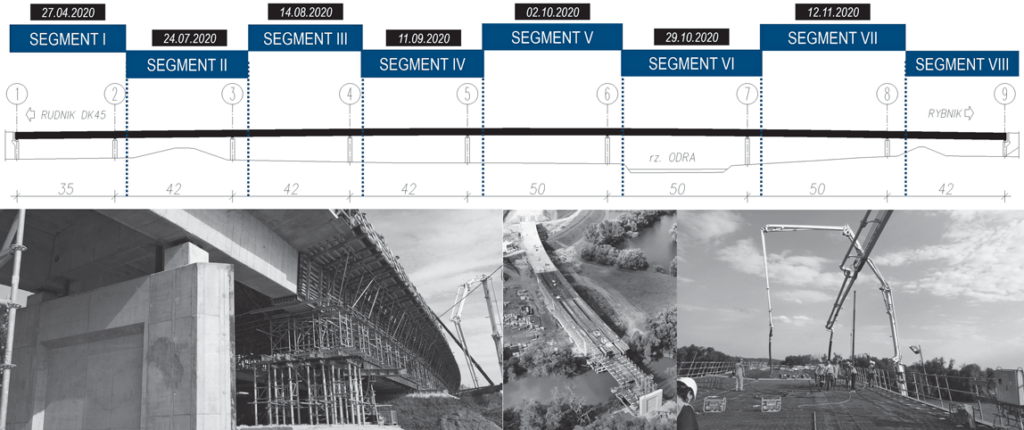
Betonowanie ustroju nośnego wykonywano przęsło po przęśle w ośmiu segmentach (ryc. 11). Wbudowywana mieszanka betonowa była kontrolowana zgodnie z przyjętym sposobem pielęgnacji próbek w warunkach znormalizowanych i odwzorowanych. Uzyskiwane wyniki badań opisaną metodą były podstawą w podejmowaniu decyzji na budowie. Poniżej przedstawiono wyniki badań dla wybranego segmentu. Na potrzeby aktualizacji modelu obliczeniowego po eliminacji odkształceń trwałych przyjęto wartość modułu E_cm,2 = 36,6 GPa określoną metodą A dla próbek pielęgnowanych w warunkach odwzorowanych.

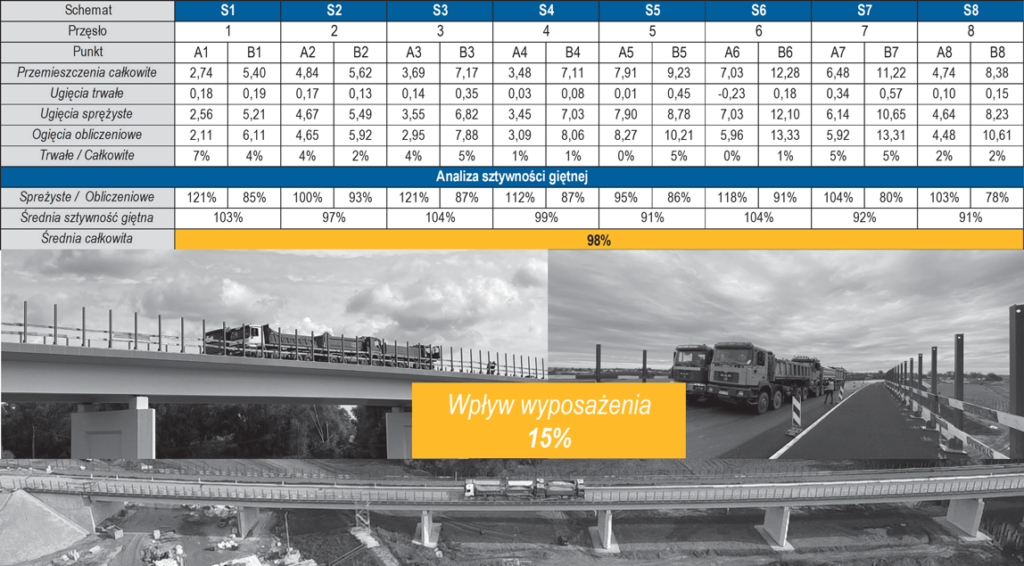
Na potrzeby weryfikacji zaproponowanej metody identyfikacji odkształcalności betonu w procesie budowy mostów 30 września 2021 r. wykonano próbne obciążenie. Zrealizowano osiem schematów przęsłowych od S1 do S8 oraz dodatkowo dwa schematy podporowe.

W tablicy 3 zestawiono ugięcia sprężyste dźwigarów A i B. Dodatkowo określono przemieszczenia teoretyczne w modelu numerycznym, w którym parametry geometryczne odwzorowano z uwzględnieniem stopnia zbrojenia. Dużą zgodność uzyskano w przypadku określania modułu ustabilizowanego metodą A w warunkach odwzorowanych (36,6 GP). Średnia relacja ugięć wszystkich przęseł wyniosła 98%. Badania porównawcze potwierdziły pracę sprężystą konstrukcji po eliminacji odkształceń trwałych, które zachodzą w momencie sprężania.

Wnioski

Zaproponowana metoda identyfikacji odkształcalności betonu w procesie budowy mostów sprężonych została zweryfikowana na podstawie analizy zachowania się konstrukcji podczas sprężania oraz przeprowadzonych próbnych obciążeń. W fazie pierwszej podczas sprężania obiektu potwierdzono skuteczność określania modułu sprężystości betonu metodą bezpośrednią na próbkach pielęgnowanych w warunkach odwzorowanych (E_cm,1 = 28,6 GPa). Uzyskana geometria przęseł potwierdzona operatami geodezyjnymi była zgodna do 1 cm z projektowaną niweletą. W fazie drugiej po eliminacji odkształceń trwałych za miarodajne uznano określanie modułu sprężystości metodą A na próbkach pielęgnowanych w warunkach odwzorowanych (E_cm,2 = 36,6 GPa). Próbne obciążenia przęseł potwierdziły zgodność sztywności giętnej na poziomie 98% w stosunku do wartości uzyskanych w zweryfikowanym modelu MES. Uwzględniając specyfikę badań laboratoryjnych betonu oraz niepewność związaną z procesem produkcji mieszanki betonowej, jej wbudowaniem oraz samą pielęgnacją stwardniałego betonu, należy przyjąć poziom ufności dla określanych cech mechanicznych betonu równy 95%. Stosowanie zaproponowanej metody minimalizuje ryzyka w procesie budowy mostów sprężonych.

Literatura

[1] Guutierrez P.A., Canovas M.F.: The Modulus of Elasticity of High Performance Concrete. „Materials and Structures” 1995, Vol. 28, No. 10, pp. 559–568, DOI: 10.1007/BF02473187.
[2] Krząkała J. et al.: Influence of Actual Curing Conditions on Mechanical Properties of Concrete in Bridge Superstructures. „Materials” 2022, Vol. 16, p. 54, DOI: 10.3390/ma16010054.
[3] Łaziński P. et al.: Innowacyjny System Monitoringu Cech Mechanicznych Betonu. „Przegląd Budowlany” 2022, t. 93, nr 5–6, s. 118–122.
[4] Skibicki S., Kaszyńska M.: Analiza wpływu wystającego z konstrukcji zbrojenia na dojrzałość betonu w czasie realizacji konstrukcji masywnych. W: Monografie technologii betonu. Kraków 2016. Materiały IX konferencji Dni Betonu (online). Stowarzyszenie Producentów Cementu. Dostępny w Internecie: https://www.dnibetonu.com/en/referaty/dni-betonu-2016-2/ (dostęp 5 lipca 2024).
[5] Krkoška L., Moravčík M.: The Measurement of Thermal Changes on Concrete Box Girder Bridge. MATEC Web of Conferences, 2016, Vol. 86, p. 01003, DOI: 10.1051/matecconf/20168601003.
[6] Neville A.M.: Właściwości betonu. Stowarzyszenie Producentów Cementu. Kraków 2012.
[7] Yang Z. et al.: A Comparative Study on the Mechanical Properties and Microstructure of Cement-Based Materials by Direct Electric Curing and Steam Curing. „Materials” 2021, Vol. 14, p. 7407, DOI: 10.3390/ma14237407.
[8] Lim K. et al.: The Time-Dependent Effect in Ultra High-Performance Concrete According to the Curing Methods. „Materials” 2022, Vol. 15, p. 5066, DOI: 10.3390/ma15145066.
[9] PN-EN 1992-1-1:2008: Eurokod 2. Projektowanie konstrukcji z betonu. Cz. 1-1. Reguły ogólne i reguły dla budynków. Polski Komitet Normalizacyjny. Warszawa 2018.
[10] PrEN 1992-1-1:2021: Design of Concrete Structures. General Rules – Rules for Buildings. Bridges and Civil Engineering Structures (draft). Technical Committee CEN/TC 250. Oslo 2022.
[11] Model Code 2010. Fédération Internationale du Béton. Lausanne2012.
[12] Model Code 2020 (draft). Fédération Internationale du Béton. Lausanne2022.
[13] Łaziński P. et al.: Wpływ cech mechanicznych kruszyw na odkształcalność mostów sprężonych w świetle Eurokodów. W: Mosty a środowisko. Seminarium Naukowo-Techniczne Wrocławskie Dni Mostowe, Wrocław, 28–29 listopada 2019. Red. J. Biliszczuk, J. Onysyk. Dolnośląskie Wydawnictwo Edukacyjne. Wrocław 2019, s. 211–219.
[14] Rüsch H. et al.: Creep and Shrinkage. Their Effect on the Behavior of Concrete Structures. Springer-Verlag New York Inc. New York 1983.
[15] Noguchi T. et al.: A Practical Equation for Elastic Modulus of Concrete. „ACI Structural Journal” 2009, Vol. 106, No. 5,
pp. 690–696, DOI: 10.14359/51663109.
[16] Krząkała J.: Wpływ kruszyw wydobywanych na terenie Polski na odkształcalność betonów. W: Ujęcie aktualnych problemów budow­nictwa. Prace naukowe doktorantów. Wydawnictwo Politechniki Śląskiej. Gliwice 2018, s. 227–236.
[17] Seruga A. et al.: Moduł sprężystości betonów na kruszywie granitowym w świetle badań doświadczalnych. „Czasopismo Techniczne. Budownictwo” 2012, R. 109, z. 4-B, s. 103–117.
[18] ACI 343R-95: Analysis and Design of Reinforced Concrete Bridge Structures (Reapproved 2004). American Concrete Institute. Farmington Hills 2004.
[19] AASHTO LRFD Bridge Design Specifications. American Association of State Highway and Transportation Officials. Washington, DC 2020.
[20] AS 3600-2018: Concrete Structures. Council of Standards Australia. Sydney 2018.
[21] CSA A23.3:19: Design of Concrete Structures. Canadian Standards Association. Toronto 2019.
[22] PN-EN 12390-13:2021: Badania betonu. Cz. 13. Wyznaczanie siecznego modułu sprężystości przy ściskaniu. Polski Komitet Normalizacyjny. Warszawa 2021.